このブログを読んでいる読者の皆さんの中に、「偏差値」を知らない人は一人もおられないでしょう。
中学受験・高校受験・大学受験と、ほとんどの模擬試験で志望校が偏差値をもとにランク付けされており、学力の指標としての偏差値は常について回ります。
受験生の皆さんは、偏差値の数値に常に一喜一憂させられているはずです。
この「偏差値」がどのように算出されているかご存知でしょうか?
なぜわざわざ「試験の得点そのもの」ではなく、よく分からない「偏差値」という数値が重視されるのか、疑問に思ったことはないでしょうか?
偏差値が必要なわけ
「得点」をそのまま指標として使えない第一の理由は、もちろん「試験の平均点が変動する」からです。
同じ70点という得点でも、平均点が60点と80点とでは全く意味が違う、というのは誰でも気付くことでしょう。
試験問題の作成者は、「なるべく平均点が一定になるような問題を作る」ように努力している場合が多いです。
難易度にブレがない方が、指標としての試験の精度がより高くなるからです。
しかしそれでも、問題作成者側が予想する問題ごとの受験者側の習熟度は、実際の習熟度とはどうしてもずれてしまい、平均点は一定ではなくなってしまいます。
そこで、平均点が多少変動しても使える指標が必要なんですね。
しかし、それなら「平均点に比べて何点高いか・何点低いか」を指標に使えばいいのではないでしょうか?
それがそうもいかないのです。なぜなら、平均点だけでなく、「得点のばらつき」も試験ごとに変動してしまうからです。
例えば、試験Aと試験Bの平均点がどちらも50点だったとしましょう。
ところが、Aの最低点は45点、最高点は65点だったのに対し、Bの最低点は20点、最高点は80点でした。こうなると、Aで60点取れたのとBで60点取れたのとでは、全く意味が違ってきてしまいます。
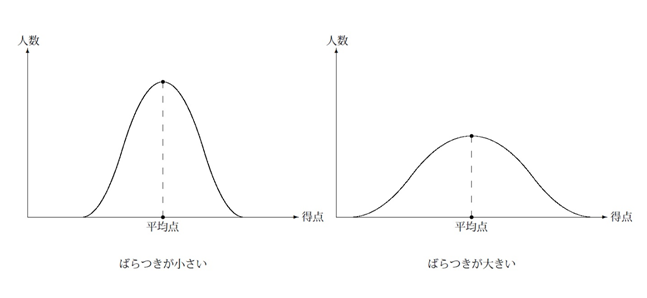
これを補正するには、「得点がどの程度ばらついているか」の指標が必要です。この指標を「標準偏差」と呼びます。
まず、(受験者の得点)-(平均点) の数値を「偏差」と呼びます(平均点より得点が低ければ偏差はマイナスになります)。
「偏差」をそのまま受験者全体で平均すると0になってしまいますが、「偏差」を二乗すると必ず0以上になるので、「偏差を二乗してから平均し、その平方根をとる」という操作を行います。
これで求められる数値が標準偏差です。
標準偏差とはつまり、「平均点からのズレの平均」だと思っていただいてかまいません。
これをもとに「偏差値」を算出します。
まず、得点が平均点ぴったりの場合を偏差値50とします。
そして、標準偏差ぶんの得点差を、偏差値10に換算します。
例えば、平均点60点、標準偏差が15点の試験があるとしましょう。
得点72点の人は平均点より12点高いので、偏差値は50+10×(12/15)=58 となり、得点51点の人は9点低いので、50-10×(9/15)=46となります。
このように計算されるので、標準偏差が非常に小さい中で平均点から大きく離れた得点の場合は、偏差値は0を下回ったり、100を超えたりすることもあるわけです。
偏差値の限界
「偏差値」は、試験ごとの難易度のばらつきをある程度補正して、学力レベルの目安を教えてくれる便利なものです。
しかし、どんな指標にも限界があるように、偏差値にもやはり限界があります。
まず、母集団が変わると偏差値の数値が示すものが大きく変わってしまう、ということがあります。
これは読者の皆さんもご存知の方が多いでしょう。
模擬試験Aで偏差値65と出るが模擬試験Bでは偏差値53になった、というのはよくあることですね。
これは、AとBでは受験者の母集団が違うからです。
それだけではありません。
偏差値というのは、「集団内のどの位置に居るか」の指標ですので、集団内で「平均点周辺の人数が最も多く、平均点から離れるに従って数が少なくなる」ような得点の分布をしているとき(正規分布に近いとき)に最も精度よく機能してくれます。
逆に言うと、そうでないとき、例えば「平均点周辺の人数が少なく、低得点と高得点の集団がそれぞれ団子になっている」というような、正規分布からかけ離れた得点分布のときにはあまり意味がありません。
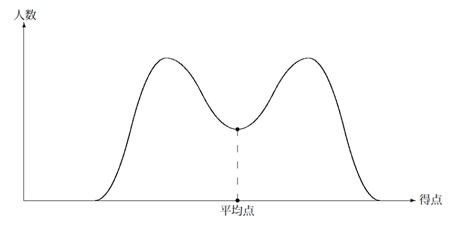
受験においては、問題のタイプや傾向も重要になってきます。
全国規模の大きな模擬試験では、あまり偏りのない、標準的な入試問題を出題することで、幅広い受験者層にとって使いやすい指標にしようとしています。
ですが実際の入試では、必ずしも標準的な問題が出題されるわけではなく、模擬試験の問題傾向とのズレが出てきます。
そうすると、模擬試験で高い偏差値が出たからといって、入試問題が解けるとは限らないという場合もあります。
「偏差値」は受験産業の歪みとしてたびたびバッシングを受けていますが、非常に優れた便利な学力指標であることは間違いありません。
しかし(あらゆる指標がそうであるように)偏差値もまた目安の一つでしかない、ということは常に忘れないようにしたいものです。












