中学数学の図形の授業では、図形の性質の証明について学習しますね。最も基本的な前提として仮定される命題を「公理」と呼び、そこから導き出される(証明される)命題を「定理」と呼びます。
この「図形の性質の証明」という数学の手法は、古代エジプトやギリシャなど、非常に古くからあるものです。紀元前3世紀ごろ、ユークリッドという数学者によって整理・体系化されたので、一般的に「ユークリッド幾何学」と呼ばれています。
ただし、中学校では普通、全ての定理を公理から証明はしません。「正確には定理だけれども、明らかな事実として扱いましょう」とする場合も多いんですね。
これはもちろん教育上の配慮です。全ての定理を公理から導き出していたら、中学校の数学の授業時間では到底追いつきませんし、難易度的にもついてこれる中学生は少数派になってしまうでしょう。中学数学の図形分野は、数学的な論理を学ぶ入門編として用意されているという側面もありますから、あまりにも難しい内容を含めるわけにはいかないんですね。
しかし、そうすると、「この内容は証明なしに使ってもいいの?」ということがどうしても出て来てしまいます。「平行線の同位角は等しい」も、そうした文脈でしばしば話題になる問題の一つです。
「平行線の同位角」のまずい証明
「平行線の同位角は等しい」の「証明」を載せているウェブサイトもあります。しかし、そのいくつかは「三角形の内角の和が180度」を利用しています。
これはちょっとまずいです。なぜなら、通常、中学数学では「三角形の内角の和が180度」を、「平行線の同位角は等しい」を使って証明しているからです。
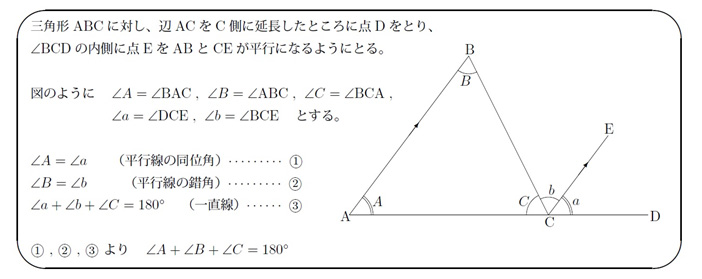
それなのに「平行線の同位角は等しい」を「三角形の内角の和が180度」を用いて導いたのでは、根本的に証明できたことにはなりません。このような誤った「証明」を「循環論法」と呼びます。
それでは、「平行線の同位角は等しい」の正しい証明はどうなるのでしょうか?
「ユークリッドの平行線公準」という難問
ユークリッドの書いた本『原論』の中には、幾何学に関する公理が列挙されています。(ユークリッドは現代でいう「公理」をさらに分類して「公理」と「公準」とに分けていますが、現代ではこのような区別をせず、全て「公理」と扱います。)これをまずは見てみましょう。
ユークリッドは図形に関する公準(公理)として、次の5つを要請するとしています。
第2公準:『線分を連続的にまっすぐどこまでも延長できる』
第3公準:『任意の中心と半径で円を描くことができる』
第4公準:『すべての直角は互いに等しい』
第5公準:『直線が二直線と交わるとき、同じ側の内角の和が2直角(180度)より小さい場合、その二直線は内角の和が2直角より小さい側で交わる』
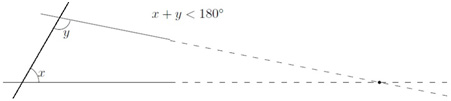
この「第5公準」を使えば、「平行線の同位角は等しい」は比較的簡単に証明できます。この第5公準のことを「平行線公準」とも呼びます。
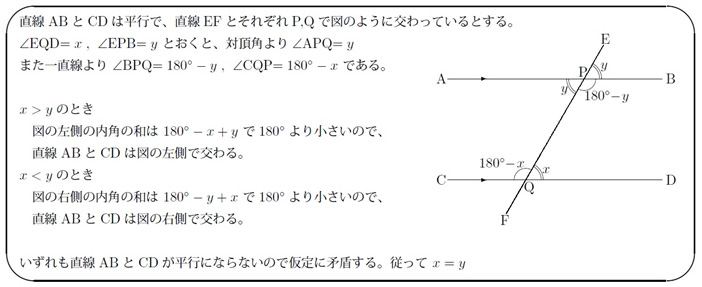
しかし、この「第5公準」は他の公理と比べてもずいぶんと内容が複雑ですし、一見して明らかとも言いにくいですよね。
実は古代の数学者たちもそう思っていました。この複雑な「公準」は、他の公理を用いて証明できる(つまり、公理ではなく定理である)のではないか? と考えたんです。
実際にプトレマイオスが証明を試みましたが、彼の「証明」は第5公準から導いた他の定理を使っており、循環論法になってしまっていました。
これ以降も数多くの数学者が証明を試みましたが、ことごとく失敗していきます。そして、『原論』からおよそ2000年もの間、「第5公準の証明」は数学上の未解決問題として残り続けたんです。
「平行線公準問題」はどう解決されたか
この問題は19世紀になって、ロバチェフスキーとボーヤイという数学者によってようやく解決されましたが、その方法は「曲面上の図形の性質を考察する」という一見すると奇想天外なものでした。
平らな平面の話をしているのに、なぜ曲がった面の話が出てくるのか? その理屈はこういうことです。
- 曲面上に「点」や「直線」や「三角形」などの図形を設定する
- ある曲面上の図形について、「第5公準」以外の全ての公理を満たすようにすることができる
- しかし、この曲面上の図形は「第5公準」だけは満たさない
この「曲面上の図形の性質」が矛盾を起こさないなら、「第5公準以外の公理」と「第5公準の否定」は両立できるということですから、第5公準は他の公理からはどうやっても証明できないことになります。こうして、「ユークリッドの第5公準は証明できない」ことが証明されました。
こう聞くと、ちょっとだまされたような気分になる人もいるかもしれません。でも論理的におかしなところはありませんし、この「証明できないことの証明」は、きちんと数学的に正しいものとして受け入れられました。

もっと分かりやすい「公理」はないか?
「ユークリッドの第5公準は(他の公理からは)証明できない」ことが証明されてしまいました。でも、第5公準が複雑で分かりにくいことには変わりありません。何とかならないでしょうか?
これと同じことを、昔の数学者も色々と考えました。その中で、ジョン・プレイフェアという数学者が、第5公準のかわりに次の公理を置いても、ユークリッド幾何学の体系がちゃんと同じように成立することを証明しています。
『ある直線と、その直線上にない点に対し、その点を通って元の直線に平行な直線は1本までしか引けない』
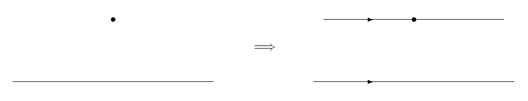
これは「プレイフェアの公理」と呼ばれています。元の「第5公準」よりだいぶ単純で、直観的に分かりやすくなった気がしませんか?
この新たな公理は広く認められ、数学者ヒルベルトがユークリッド幾何学をさらに厳密に整理する際にも採用されています。
最初から『原論』にこの公理が採用されていれば、ユークリッド幾何学の体系は最初からもっとすっきりしたものになっていたでしょう。しかしそうすると、「平行線に関する公理が証明可能ではないか」という疑問も生じず、非ユークリッド幾何学の誕生はもっと遅れていたかもしれません。
「こんなにすっきりした表現ができるなら、中学数学でもこれを公理として教えればいいのに」と思う人も居るかもしれません。ですが、それには一つ問題があるんです。
さっき第5公準を使った証明をしましたが、この「プレイフェアの公理」を使って「平行線の同位角は等しい」を示そうとすると、はるかに証明が長く、面倒くさいものになるんです。最初に言ったように、中学数学ではあまりにも難しい内容を扱うわけにはいかないので、ふつう中学校ではこれを公理として紹介していないんですね。
この証明は改めて別の記事で紹介しましょう。長くて面倒とはいえ、中学数学の図形の証明の基本だけでちゃんと証明できますので、図形の証明に自信がある人は挑戦してみても良いかもしれません。
上記の問題はもともと生徒からの質問でした。当塾では生徒一人一人に合わせた授業を行っております。成績を上げたい、自分も質問してみたいとお考えであれば気軽にお問合せください。
お問い合わせは → こちら から












