今回はグラフの少数と分数と整数の不思議なお話し。 ある生徒からの質問が来ました。
生徒の質問

この類の質問は昔からよく受けていたが、今回改めて書くことにしました。この質問は中学生から受けたものですが、小学生や中学生の知識の範囲では答えることができません。
最低限でも高校の数学の知識が必要です。とは言え、高校数学の知識があってもわからない人が沢山います。
この生徒の問題点を整理すると、1 と 0.99999 · · · という2つの違った表現のものが何故イコール(=) なのか。です。つまり疑問点はイコール (=) にあります。
イコール (=) とは一体何者?その事例
このような疑問を持つ人はほとんどいませんが、今この問題の原因がイコールにある以上、イコールを考える必要があります。
そこでまずはイコールが使われている事例から。

答えは、 りんご 1 個とみかん 2 個買ったので、買ったのは全部で 3 個になりました。 と言えます。
この事例でのイコールの意味は、 『~になる』 に相当します。
「1 + 2 で 3 になる」の 『~になる』 に相当します。
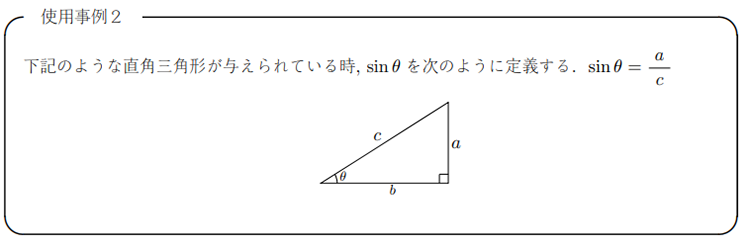
数学I教科書なんかにはこのように書かれているが、この時のイコールは 『~と定義する』 を表しています。
大学の数学科では、「定義」の意味でイコールを使う時、イコールの意味の誤解を招かないように、
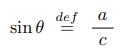
のように表す。ただし、def は definition(定義)を省略したものです。

この内容は高校 3 年生、学校によっては高校2年生や高校1年生で習うこともあるが、文部科学省が規定している範囲では高校3年生で習い範囲。
この数式の解釈は、「x を α に近づけると、f(x) は f(α) に近く」という解釈になります。つまり、今問題になっているイコールの解釈としては 『近く』 になります。
「近く」とは、その値にどこまでも近くに行くことを表しますが、あくまでも「近く」だけで、その値が「ある」かどうかは不明です。
結局、イコールって?
今イコールの解釈を一部紹介しましたが、イコールには様々な意味合いを持っています。数学の論理の展開の状況に応じて、解釈が変わります。
英語で言うところの『多義語』に当たります。つまり1つの英単語に対して1つの日本語が対応しているのではなくて、1つの映単語に対して、文脈に応じて対応する日本語が、色々と変わるものと同じです。
イコールについても同じで、状況によって意味合いや解釈が変わります。
数学における無限の表現
数学においては、無限の表現が決められています。数学では無限(終わりの無いもの)は有限(終わりがあるもの)の極限(lim)で定義します。
数学における「定義」とか数学をする上での決まり事です。
この中学生の質問の答え
![]()
となります。
つまり、終わりの無い 0.99999 · · · は 1 と定義すると言う意味で、 0.99999 · · · が、計算上 1 になると言う意味ではありません。
念の為、計算式は載せますが、小学生、中学生にはちょっときついと思います。2019 年現在では高校の数学 III で習う範囲です。
ちょっと丁寧めに書きます。(不要と思う人は飛ばしてください。)
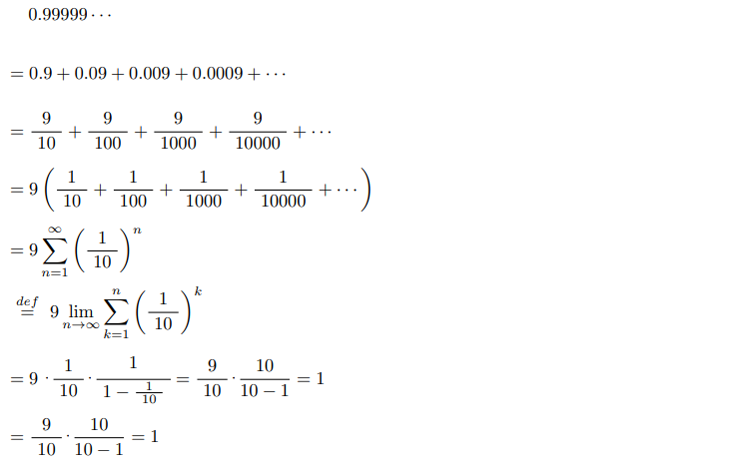
必要な人は参考にしてね!












